📢 大家好,我是小丞同学,一名大二的前端爱好者
📢 这篇文章将讲解数据结构中的树
📢 非常感谢你的阅读,不对的地方欢迎指正 🙏
📢 愿你忠于自己,热爱生活
💡 知识点抢先看
- 什么是树结构?
- 树的相关术语
- 树结构有哪些类型
- 树的前中后序遍历
- 树的层序遍历
- 手写实现一颗树
一、什么是树结构?
树和哈希表一样是一种非顺序的数据结构,它对于存储需要快速查找的数据非常有用
树是一种分层抽象模型,可以理解为一层一层的,就类似于高中生物的遗传图谱
如下图所示
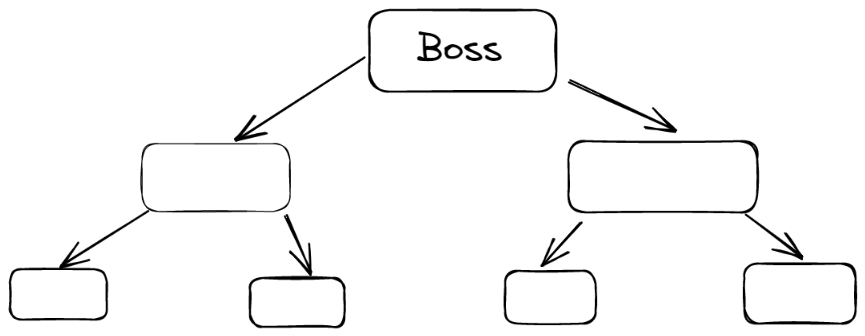
二、树的相关术语
根据上面的图,我们大致知道了树是一个怎样的数据结构,虽然对于实现它还一头雾水,现在我们先来了解一下关于树的相关术语
首先我们先列个表
| 术语 | 含义 |
|---|---|
| 节点 | 书中的每一个元素都叫节点 |
| 节点的深度 | 它的祖先节点的数量 |
| 树的高度 | 所有节点深度的最大值 |
| 内部节点 | 至少有一个子节点的节点 |
| 外部节点 | 没有子元素的节点 |
| 节点的度 | 节点拥有的子树个数 |
| 叶子节点 | 度为 0 的节点 |
接下来我们来详解一下这些分别是什么意思
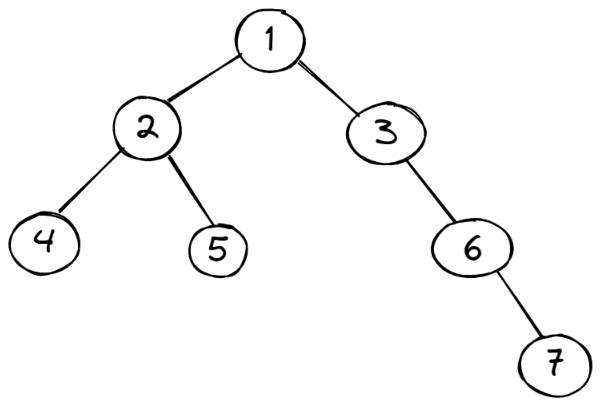
首先位于树顶部的节点,称为根节点,它不存在父节点,也就是节点 1
树中的每一个元素都叫做节点
没有子元素的节点又叫做外部节点,例如图中的 4,5,7 这几个节点,它们都不存在子元素
剩下的节点都是内部节点
节点中有一个属性叫深度,它取决于祖先节点的数量,例如图中的节点5,它有2个祖先节点,分别是 2 和 1 ,因此它的深度就是2
对于一棵树而言,它有高度可言,高度取决于节点深度最大的值,也就是节点 7,它的深度是3,因此这颗树的高度为 3
节点的度,度表示的是节点拥有的子树的个数,例如节点1,有两颗子树,因此节点1的度为2,对于节点3而言,它只有一颗子树,因此节点3的度为1
对于叶子节点,也就是度为0的节点,也就是没有子树的节点,例如图中的节点 (4,5,7),这些都称做叶子节点
三、树结构有哪些类型
对于树来说它千变万化,它有着很多种形态,例如
最常见的二叉树,二叉搜索树
当然它还有
- 红黑树
- avl 树
- n 叉树
- 平衡二叉树...
还有很多种类型,这里主要就讲二叉树,因为其他的有点难,还没有学
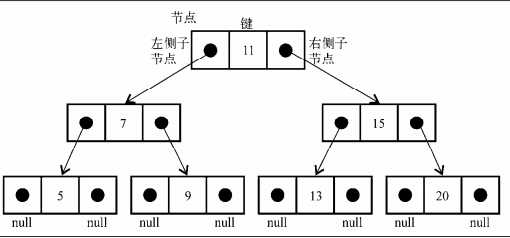
二叉树:节点最多只能有两个子节点,一个是左侧节点,一个是右侧节点,如图就是一棵二叉树
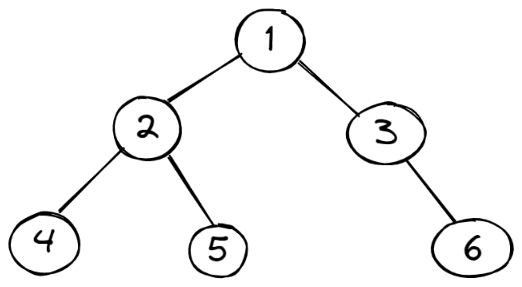
二叉搜索树:左侧节点存储小的值,右侧节点存储大的值,因此也就是从左到右,从小到大,如图就是一棵二叉搜索树
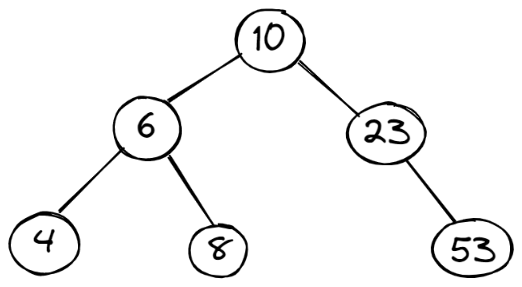
四、树的前中后序遍历
对于树的遍历,我们有三种常规的方法,前序遍历,中序遍历,后序遍历
1. 前序遍历
前序遍历的顺序是:根节点 -> 左子节点 -> 右子节点,对于子树而言也是按照这个规律来遍历,如图所示

自己尝试用代码实现一下噢~~
2. 中序遍历
中序遍历的顺序是: 左子树 -> 根节点 -> 右子树,如图所示
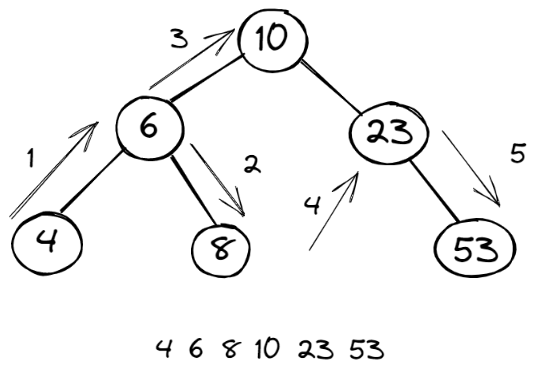
递归代码实现
const inorder = (root) => {
if(!root) { return }
inorder(root.left)
console.log(root.val);
inorder(root.right)
}3. 后序遍历
后序遍历的顺序是:左子树 -> 右子树 -> 根节点,如图所示
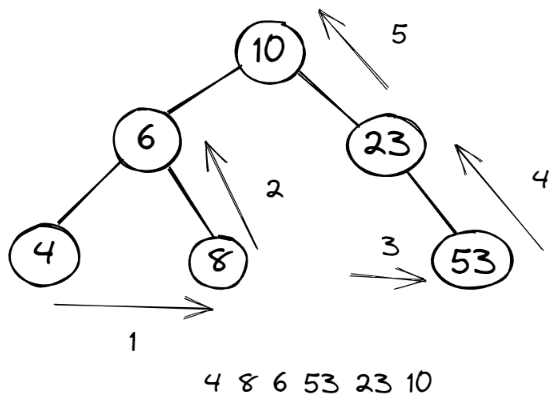
const postorder = (root) =>{
if(!root) {return}
// 先访问左子树,再访问右子树
postorder(root.left)
postorder(root.right)
// 最后访问根节点
console.log(root.val);
}前序遍历代码如何实现呢?自己尝试一下吧~递归和迭代都可以试试噢
五、树的层序遍历
在 LeetCode 刷题中,经常会有这样的题目,需要按照层级来遍历,是什么意思呢
它的意思是:逐层地,从左到右访问所有节点
也就是按照图中的方式来遍历,并且返回结果
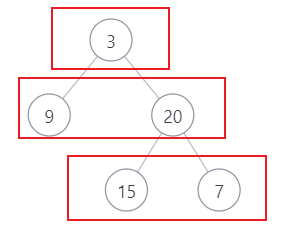
返回结果: [ [3], [9,20], [15,7] ]
也就是把每一层的元素放在一个数组中返回,如何实现呢?
- 首先我们需要在广度优先遍历的基础上,添加层级的判断
- 记录下当前层级的节点数,当当前层级遍历完成之后,从下一个数组继续遍历
var levelOrder = function (root) {
// 空树
if (!root) return []
// 队列 广度优先遍历,[根节点,层级]
const q = [
root
]
const res = []
while (q.length) {
// 记录一下当前有多少个节点是上一次循环遗留的,这些节点就是当前层级的全部节点
let len = q.length
res.push([])
// 将这些节点全部出队
while (len--) {
const n = q.shift()
res[res.length - 1].push(n.val)
if (n.left) q.push(n.left)
if (n.right) q.push(n.right)
}
// 在下一次的外层循环中,又会新创建一个新的空数组
}
return res
};六、二叉搜索树有哪些方法?
在这里就罗列几个常见的方法吧
| 方法 | 作用 |
|---|---|
insert | 向二叉搜索树中插入数据 |
serach | 查找某个值 |
remove | 移除某个值 |
还有很多比如返回最大值,返回最小值的方法,都可以实现,这里就不写那么多了
七、手写实现二叉搜索树
1. 创建 Node 类
创建一个节点类,用来实例化创建新节点,二叉搜索树最多只有两个节点
通过这个类来创建节点,默认为 null ,有 left,right 两个子节点都为 null
class Node {
constructor(data = null, left = null, right = null){
this.data = data
this.left = left
this.right = right
}
}2. 创建 BinarySearchTree 类
用来添加整棵树的方法
class BinarySearchTree {
constructor() {
this.root = null
}
}3. 实现 insert 方法
insert 方法实现插入一个元素,根据二叉搜多树的特性,左子树值小于右子树值,我们需要设计出合理的插入方式
- 首先我们需要创建一个新节点,并且传入
data及节点数据 - 如果插入的是第一个节点,那么该节点就是根节点
- 如果不是第一个插入的节点,那么我们需要通过一个函数来辅助实现插入
insert(data) {
const newNode = new Node(data)
// insertNode为辅助函数
this.root === null ? this.root = newNode : insertNode(this.root, newNode)
}在这里我们写好了 insert 方法,简单的逻辑判断,根节点有无,接下来的处理交给 insertNode 函数来实现
如何实现呢?
根据二叉搜索树的特性,我们采用递归的方式
- 首先先判断传入的节点和根节点的大小关系
- 如果比根节点小,则放到左子树,反之
- 如果当前左(右)子树为空,则它直接成为左树第一个节点
- 如果不为空,我们接着比较它和左(或右)子树的大小关系,实现递归
function insertNode(node, newNode) {
// 如果值小于根节点,插到左子树
if (newNode.data < node?.data) {
// 如果没有左子树,那么直接是左节点
if (node.left === null) {
node.left = newNode
} else {
// 递归
insertNode(node.left, newNode)
}
}else {
if(node.right === null) {
node.right = newNode
}else {
insertNode(node.left,newNode)
}
}
}这样我们就实现了一个 insert 方法,我们来看看如何使用吧~ 随便测试一下
const tree = new BinarySearchTree()
tree.insert(344)
tree.insert(31114)
tree.insert(324)
tree.insert(34)看到调试器面板中的记录,符合我们的预期
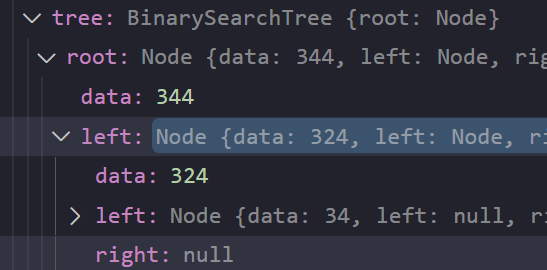
我们再来看看插入是如何一步一步实现的吧~
const tree = new BinarySearchTree()
tree.insert(15)
tree.insert(31)
tree.insert(6)
tree.insert(48)
4. 实现 search 方法
search 方法需要接收一个查找的值,我们返回 true 或者 false ,这和之前的 has 方法类似,那我们该如何实现呢?
同样的我们需要借助一个辅助函数来实现
- 首先,我们先声明
search方法,传入树和需要查找的值 - 当我们的树为空时,说明一定不可能查找到值
- 当查找的
data小于根节点的data时,我们需要递归左子树继续判断 - 当大于根节点时,递归右子树判断
- 如果刚好等于根节点就返回
true
实现 search 方法
search(data) {
return searchNode(this.root, data)
}实现 searchNode 方法来实现查找
function searchNode(node, data) {
if (node === null) {
return false
}
if (data < node.data) {
return searchNode(node.left, data)
} else if (data > node.data) {
return searchNode(node.right, data)
} else {
return true
}
}实现效果如何,我们来试试
const tree = new BinarySearchTree()
tree.insert(59)
tree.insert(29)
tree.insert(48)
tree.insert(18)
tree.insert(79)
tree.search(48)
tree.search(1)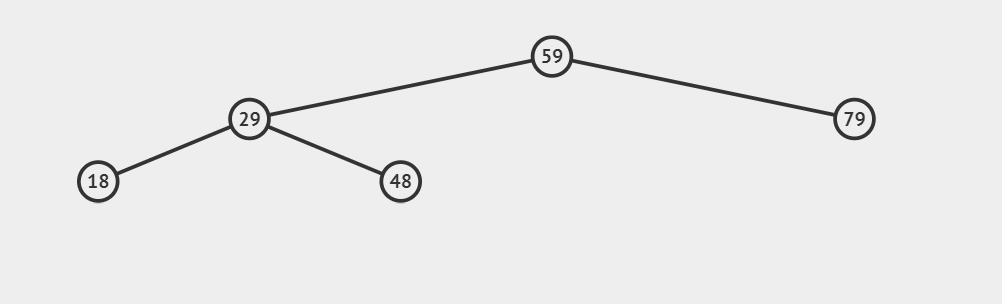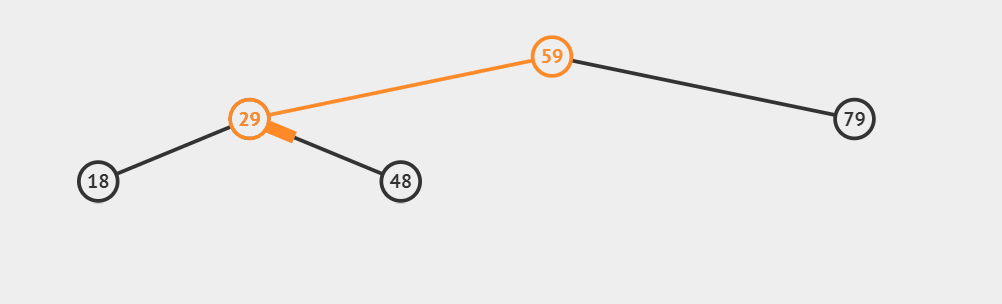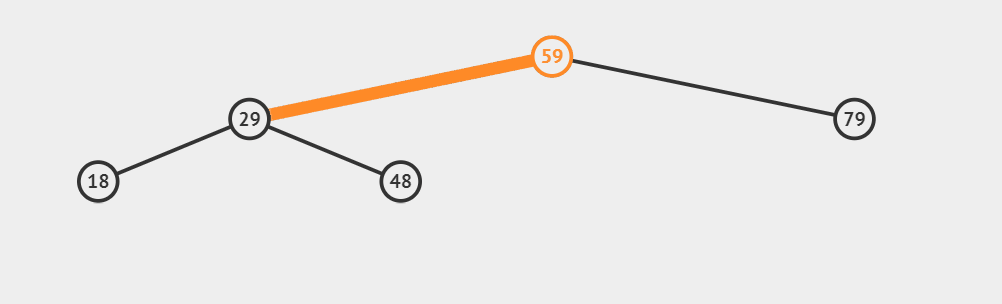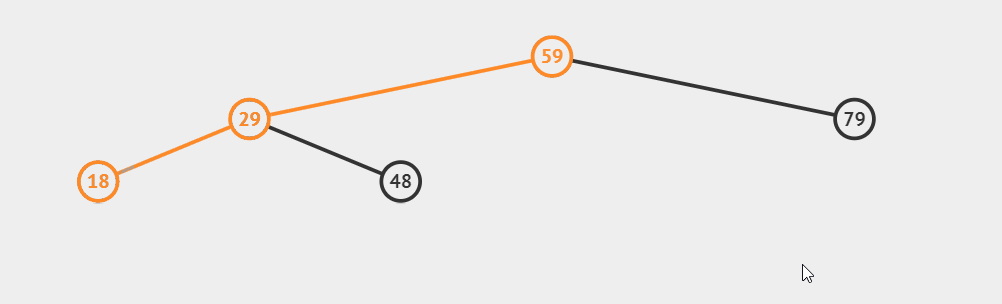
5. 实现 remove 方法
remove 方法删除节点,这个方法是最复杂的一个方法,它要考虑的东西有很多
对于删除节点,可以分为三种类型
- 删除叶子节点
- 删除的节点只有一个子节点
- 删除的节点有2个子节点
如何实现,我们一步步来看
首先我们需要实现一个 removeNode 函数,来保证我们的类中的干净,我们先声明这个 remove 方法,在这里我们预定 removeNode 需要返回根节点
remove(data) {
this.root = removeNode(this.root, data)
}来实现 removeNode 方法
首先我们先处理一些边界判断的工作
在这里我们先处理了空树的情况,当树为空时返回 null 即可,接着我们对需要删除的节点进行了搜索,这里利用的是递归实现的,当我们找到了这个节点时,当前的 node 就会指向了要删除的节点,然后进行判断
function removeNode(node, data) {
if (node === null) return null
if (data < node.data) {
node.left = removeNode(node.left, key)
return node
} else if (data > node.key) {
node.right = removeNode(node.right, key)
} else {
// 三个情况
}
}第一种情况:删除叶子节点,也就是 left,right 都为 null 时,可以直接删除,让当前节点 node = null 即可
if(node.left === null && node.right === null) {
node = null
return node
}
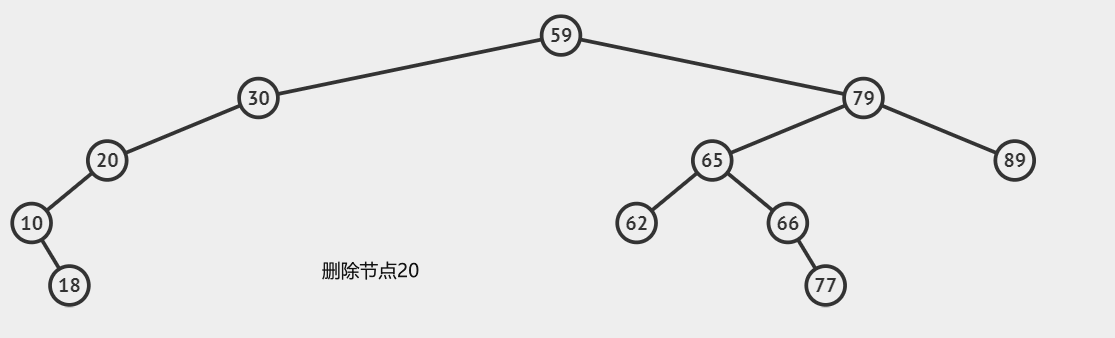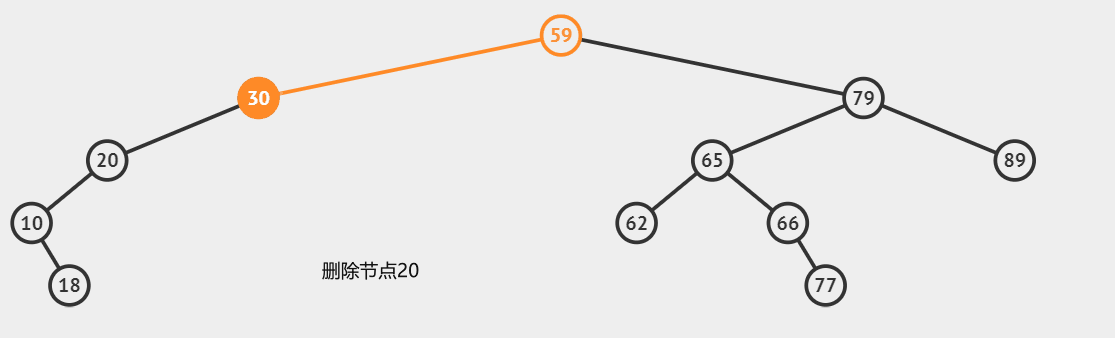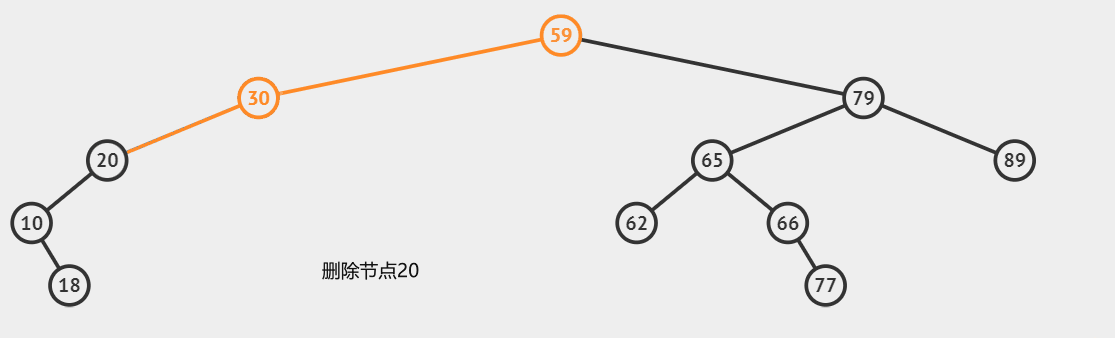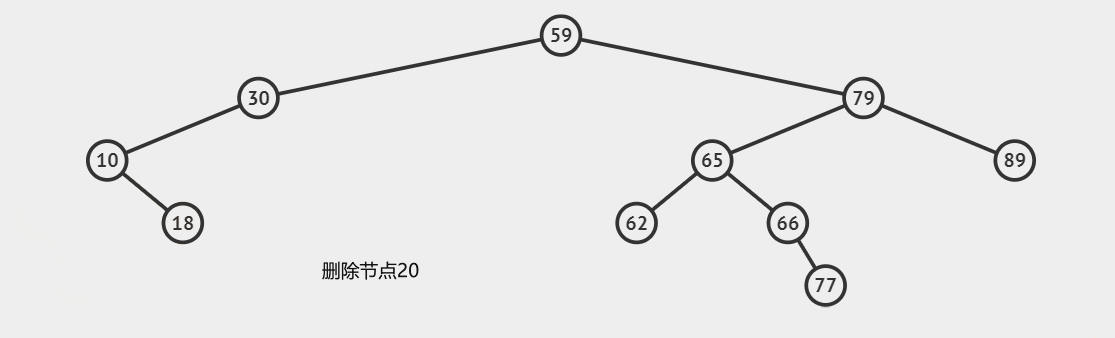
第二种情况:删除只有一个子节点的节点
这种情况下,我们需要跳过当前节点,指向它的子节点,也可以说是用子节点替代它的位置
if(node.left === null) {
node = node.right
return node
}else if(node.right === null) {
node = node.left
return node
}
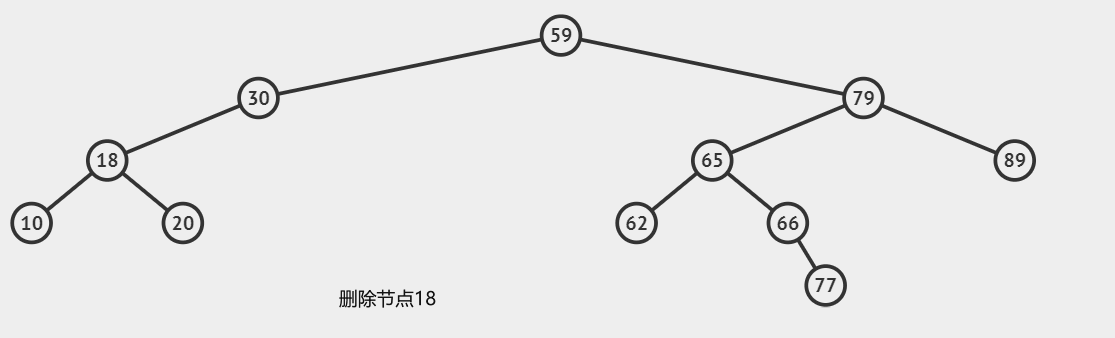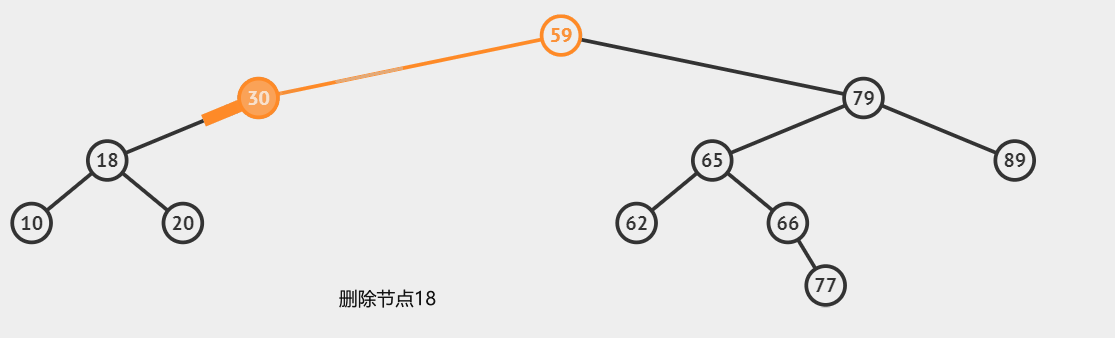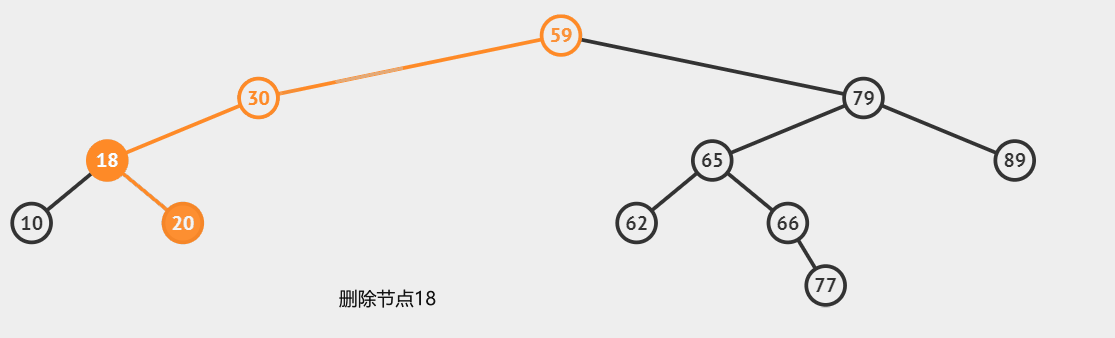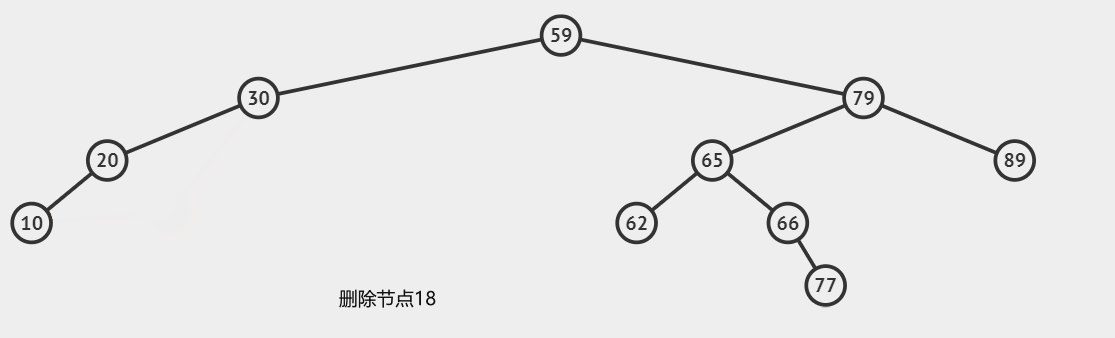
第三种情况:删除两个子节点的节点
这种情况是最复杂的
- 找到该节点的右子树中的最小值
- 然后用这个最小值,去替代当前的这个被删除的节点
- 之后我们需要删除右子树中的那个节点
- 最后返回更新后节点的引用
在这里我们使用了一个自己封装的方法 findMinNode ,可以自己去试试如何实现,它的功能是,返回最小值的节点
const min = findMinNode(node.right)
node.data = min.data
node.right = removeNode(node.right,min.data)
return node这样我们就实现了这三种情况的判断,结合起来就可以正常工作了
到这里我们实现了几个很常用的方法,难度还是蛮大的,需要自己多练练
八、LeetCode 实战
以下这些 leetcode 题可以去尝试一下
104. 二叉树的最大深度
111. 二叉树的最小深度
102. 二叉树的层序遍历
112. 路径总和
96. 不同的二叉搜索树
98. 验证二叉搜索树
99. 恢复二叉搜索树
226. 翻转二叉树
这些题都可以去尝试一下哦~
📖 总结
在这篇文章中我们从什么是树开始,最后封装了一颗二叉搜索树,难度还是有的,做树相关的题目,必须要理顺我们的思路,采用递归要确定好递归顺序。在我们做题的时候,不必封装一个完整的树,只需要我们知道有这个数据结构,在我们需要使用的时候,我们提取它的灵魂即可,学了这么多的数据结构,也能发现,它们都是通过数组或者对象封装而成的,因此它们的本质还是我们最熟悉的东西。
本文关于树的内容就到这里结束了,相信你一定能从中学到很多东西。下一篇文章将带你探索堆的奥秘。
欢迎大家关注本专栏,持续关注最新文章~
最后,可能在很多地方讲诉的不够清晰,请见谅
💌 如果文章有什么错误的地方,或者有什么疑问,欢迎留言,也欢迎私信交流